|
|
主题: 全世界几百年来错误的透视原理(绘画透视)
|

双子座
职务:普通成员
等级:1
金币:0.0
发贴:625
注册:2008/2/2 9:33:14
|
#162008/11/28 13:15:31
图片如下: 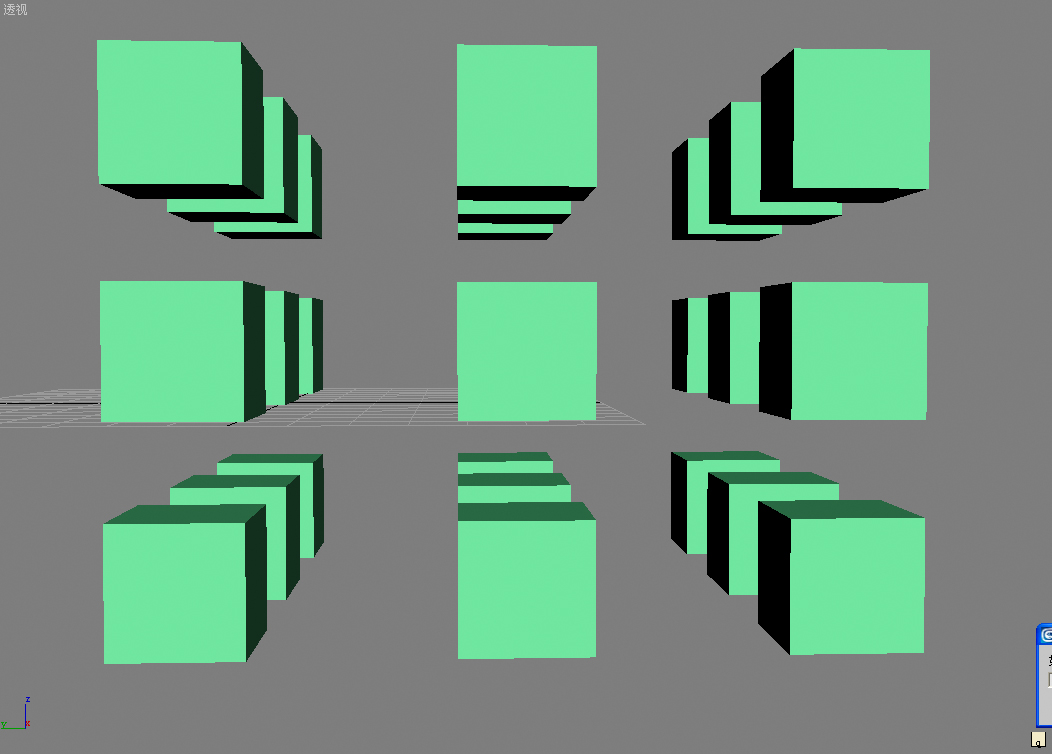
|

文子
职务:普通成员
等级:1
金币:0.0
发贴:20
注册:2006/8/7 18:15:14
|
#172008/11/29 18:36:56
回SII:
首先我要声明一点,我没有另立门派的意思,更不存在偷用经典透视法的说法,
我的研究都是建立在经典透视法基础上的开发新的理论,也可以说是在完善经典透视法。
当然写这个篇文章的主题有点过份,如果我写成《关于透视的一点研究》有多少人会看?
我的目仅仅只是为了吸引眼球,让更多人关注本贴.我只是把我的发现写出来,供大家绘画时,
有个参考方向,让更多人作出的作品更加接近真实,,我怎么可能在做无用功呢?
并不是前人所有的东西都是对的。国内的很多教材都有谬误也很正常。经典透视摆在那里,没错
但不是所有的我都用,对的我肯定要用,如三点透视,我一直在用。但错的我也要用吗?
关于房间里有两个方块的例子,不属于我所说的室内透视的说法,那又是另一种物体了,就不能把房间的方块
也画成一点透视,看到几个面就要画成几点透视,除非你要画方块内部的透视。所以有了我这个理论后,就可以
纠正很多人不要再犯那种错误,不再把它们画成一点透视,你说有没有意义呢?
按你的道理,正方体的高度可以忽略不计算,为什么长度的宽度也不一起忽略不计算?因为我们都知道正方体12边都是相等的
那样是不是就不用再画透视了?
最后我想再纠正一下,我没有想取代经典透视,我只是在完善经典透视。如果按经典透视的画法,图9采用的是两点透视,是没有错的,但是你看一下效果,理论上没错,为什么我们感觉是有点别扭?头重脚轻?如果你偏要说你没感觉我也没办法。
|

文子
职务:普通成员
等级:1
金币:0.0
发贴:20
注册:2006/8/7 18:15:14
|
#182008/11/29 18:51:30
回楼上的双子座 图片如下: 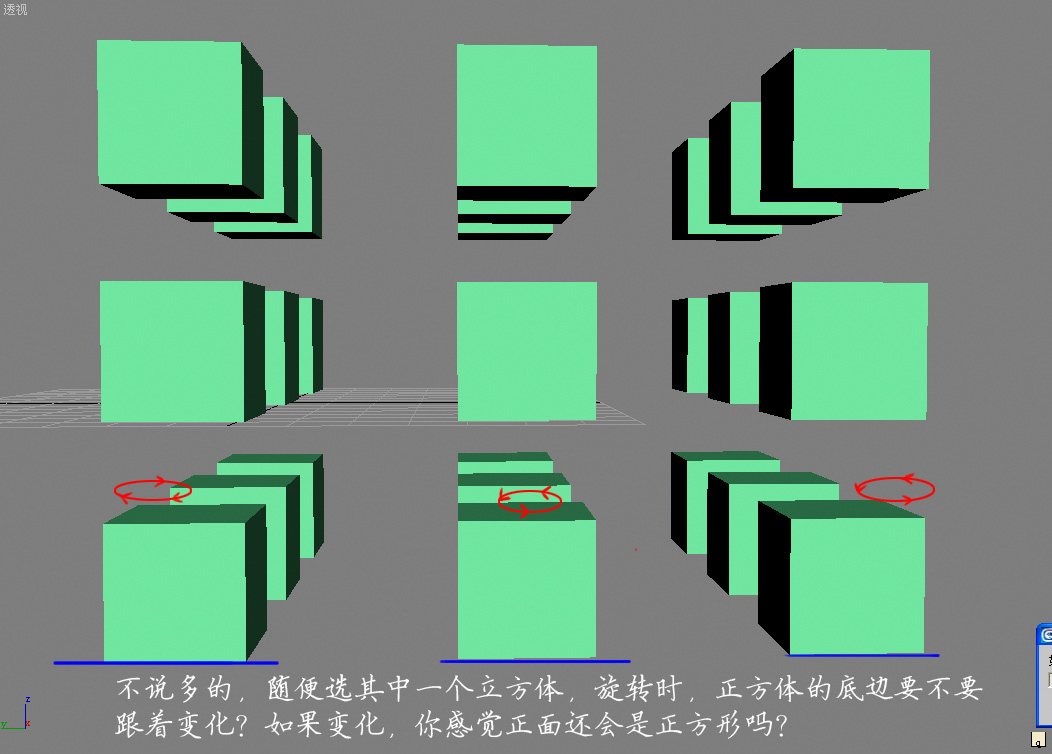
编辑历史:[此帖最近一次被 swf123 编辑过(编辑时间:2008-11-29 18:56:49)]
|

guttersnipe_5d
职务:普通成员
等级:2
金币:0.0
发贴:66
注册:2005/12/20 10:47:42
|
#192008/11/29 19:11:25
swf123在上个帖子中说 - 引用:
- 回楼上的双子座
图片如下:

当正方体旋转时,一旦底边与视平线不平行就变成2点透视了,正面自然不会是正方形,是产生了透视的正方形的面
|

小葱拌豆腐
职务:普通成员
等级:5
金币:0.0
发贴:62
注册:2006/8/8 14:52:05
|
#202008/11/29 21:22:15
如果你不是无知,我感到你有点胡搅蛮缠了。人家解释你这个,你又去说那个。那图明明说的是在一个房间多个正方体与水平线垂直的情况,用以驳斥你的一点透视说。并且还直接告诉你:1点透视本来就不计算水平的平行线的透视关系。你无以还击,就用旋转正方体弄出个新题目来逃避反思。旋转了就不是一个灭点了,也不叫一点透视了。瞎搞什么你?痴迷是可爱的,一根筋瞎追就花痴了。
编辑历史:[此帖最近一次被 gulanshi 编辑过(编辑时间:2008-11-29 21:27:23)]
豆腐娘子,有一点小聪明。小聪明常常坏大事,所以只干小事不敢做大事。
|

SII
职务:普通成员
等级:1
金币:0.0
发贴:7
注册:2008/11/27 2:47:41
|
#212008/11/30 11:36:06
其实那些透视没有错,是楼主自己没用对方法,没有理解透彻。『看到几个面,就画成几点透视』不得不说这是很错乱的方法,这样根本无法建立一个严密的透视空间。1点2点透视各自都是一个完整的体系,它们不计算与视平面平行的高或者宽,是构成基本模型的前提条件而以。 引用:『...那又是另一种物体了,就不能把房间的方块也画成一点透视,看到几个面就要画成几点透视,除非你要画方块内部的透视...』 楼主这么说,干嘛不去验证一下?你试试把那左右两边的方块画成2点透视或3点透视?在同样一个画面中,最终那样只会和那个1点透视的房间相互矛盾,这样不是更加别扭么?所以说楼主的透视法有点混乱,把几种透视法杂技在一起肯定不行的。 1点2点透视相对不真实,但为什么错?古代很多大师用1点2点透视画的油画太多了。我前面已经说了,楼主一直在用和“真实”比较来指出经典方法的错误,是很狭义的论断。客观说应该是,每种方法的“保真度”不同。如同我们有了爱因斯坦的理论后,也不会去否定牛顿的存有较大误差的定理,日常的力学运动用牛顿的已经足够。只是每种方法理论所作用的范围不同罢了。 我一直在强调透视法是各种不同的“方法”,楼主可能根本没看进去。没有人规定只能用一种方法来做透视吧。你要真实效果,就用真实的方法去画,根本没必要去批其它对你而言用不着的方法。产品设计,工程制图,建筑设计上1点2点透视用得太多了,你难道都批判它们是错的? 不罗嗦了,这里有个资源,介绍了有史以来所有的透视法,从1点到6点,是个研究透视的学者弄的,真有心的话可以弄来看看。透视法其实来来去去就那几个,坛子里有个写透视的帖子也介绍得比较详细。 www.termespheres.com/perspective.html
|

文子
职务:普通成员
等级:1
金币:0.0
发贴:20
注册:2006/8/7 18:15:14
|
#222008/11/30 16:27:21
gulanshi在上个帖子中说 - 引用:
- 如果你不是无知,我感到你有点胡搅蛮缠了。人家解释你这个,你又去说那个。那图明明说的是在一个房间多个正方体与水平线垂直的情况,用以驳斥你的一点透视说。并且还直接告诉你:1点透视本来就不计算水平的平行线的透视关系。你无以还击,就用旋转正方体弄出个新题目来逃避反思。旋转了就不是一个灭点了,也不叫一点透视了。瞎搞什么你?痴迷是可爱的,一根筋瞎追就花痴了。
不知道是我花痴还是你花痴,发个贴我是好心的,本不想骂人,请说话客气点。 是你不理解我的意思,我为什么要旋转,我只想告诉他就是一点透视的立方体根本就不存在(室内除外)。以后老师讲课不要再拿立方体来给别人讲一点透视,根本就讲不通的,要讲一点透视,画个平面的就行了。明白不?你脑子怎么还老转不过弯呢
|

guttersnipe_5d
职务:普通成员
等级:2
金币:0.0
发贴:66
注册:2005/12/20 10:47:42
|
#232008/11/30 16:27:41
其实楼主要是一开始持一个低调理性的姿态来探讨,倒也无妨
结果从题目到开篇第一句话,处处透着自己能个儿,心态不好
|

文子
职务:普通成员
等级:1
金币:0.0
发贴:20
注册:2006/8/7 18:15:14
|
#242008/11/30 18:58:20
回楼SII 要验证,你自己拿相机去照。我没闲功夫去画。 不过这几天我倒发现了很多透视中的矛盾。我得好好研究一下,我很佩服那个指出曲线透视原理的大师,他的理论解开了我的一些困惑。 我不想跟你扯得太远,我的是错的你不要采用就是了,以后你教你学生做作品时,就画这成这样的效果 一点透视原理 图片如下: 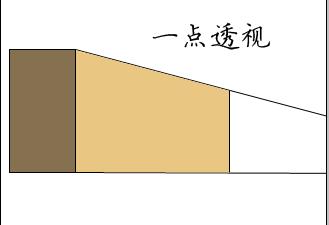 一点透视原理的实际应用效果 图片如下:  不要画成下面这样的效果,因为我的是错的。 图片如下: 
编辑历史:[此帖最近一次被 swf123 编辑过(编辑时间:2008-11-30 19:26:24)]
|

文子
职务:普通成员
等级:1
金币:0.0
发贴:20
注册:2006/8/7 18:15:14
|
#252008/11/30 19:25:14
guttersnip在上个帖子中说 - 引用:
- 其实楼主要是一开始持一个低调理性的姿态来探讨,倒也无妨
结果从题目到开篇第一句话,处处透着自己能个儿,心态不好
你指点的有理,但你址到心态不好,我就不服了,你知道吗,中国千百年来有多少高人? 他们在默默在研究谁能发现?,到最后导致多少技术失传? 当然我不能跟那些高人相比并论,我用的题目和说话的方式只不过是换一种方式吸引更多人来相互学习,这与心态好不好无关。这只是一种方式。
|

woodbind
职务:普通成员
等级:1
金币:0.0
发贴:451
注册:2008/6/2 11:15:17
|
#262008/12/1 10:49:39
上面小下面大的房子感觉空间被扭曲了~
这个感觉就像地平面看起来是直线,实际上是曲线。可是大部分情况下感觉还是直线?
传统的透视可能是一种大部分情况下的近似。就像我们用欧几里德几何一样~又或者像牛顿力学一样
楼主用的是像使用黎曼几何一样的感觉,突出了空间的张度,有点鱼眼的感觉。感觉只有非常高的楼,在某种观察角度才有这种感觉。
|

SII
职务:普通成员
等级:1
金币:0.0
发贴:7
注册:2008/11/27 2:47:41
|
#272008/12/1 12:18:40
回复swf123: 讲了这么久还真是较起真来了···呵呵 任何情况下我只会告诉学生使用更正确和科学的方法,当然一点要我亲自证明给大家看的,经得起推敲的。 第一个图: 从图上看,假设这个房子是与投影平面平行的,那么画成那样的一点透视又有何错?一点透视的别名就称为"平面透视"。更何况这样情况下的一点透视根本不是完整的构图,偏离中央视心很远了当然有严重变形,任何透视的构图偏离到一定程度都会有严重变形,但如果把整个1点透视画完整,那么就会表现出1点透视的大气庄重感,去看看那些1点透视的古典油画就知道了。如果这个房子实际上是成角的,而楼主非要给给它按一个1点透视来表现,然后指出1点透视是错的,那这样的讨论就没有意义了吧。 第二个图: 这个房子已经与投影平面成角了,当然用2点透视更合适,所以两点透视有个别名又叫"成角透视". 其实,成角立方体的透视不是也可以用3点透视来画么。 总来说,一个房子成角,另一个平行,表达对象都不同,哪来可比性?楼主举这个例子等于又把1点2点透视各自的概念重申了一遍,如果再把该房子3点透视的效果图也列举出来,这样3种经典透视的对比应用实例也就齐了·· 总之我觉得楼主所谓发现的理论,其实是在有选择地片面地重复原经典透视的原理。抱着这样的态度去研究经典透视,当然觉得矛盾。 我之前说验证根本用不着相机,而且楼主一直以来讲的也不是完全和真实透视的原理相关的。再提一遍,1点2点3点透视仅仅只是经典的一种制图和绘画的方法,用在哪里怎么用都是有规定的,应该各自作为完整的体系来使用,不能像楼主那样随意拆解混用。真实看到的透视本身就是曲线性(外加镜头本身的曲光率)所以照相机拍的真实世界只会是曲线透视,1点2点3点透视是解释不了的。 楼主应该去看看3d游戏或3d cg原理里的摄像机是怎么编出来就懂了。 它的数学模型其实就是一个“平截头体”的空间投影在一个平面上的数学公式,这样压缩后投影出来图像会把线性轮廓的物体根据空间位置呈现出一定的曲率。简单的示意图就是这样: 图片如下: 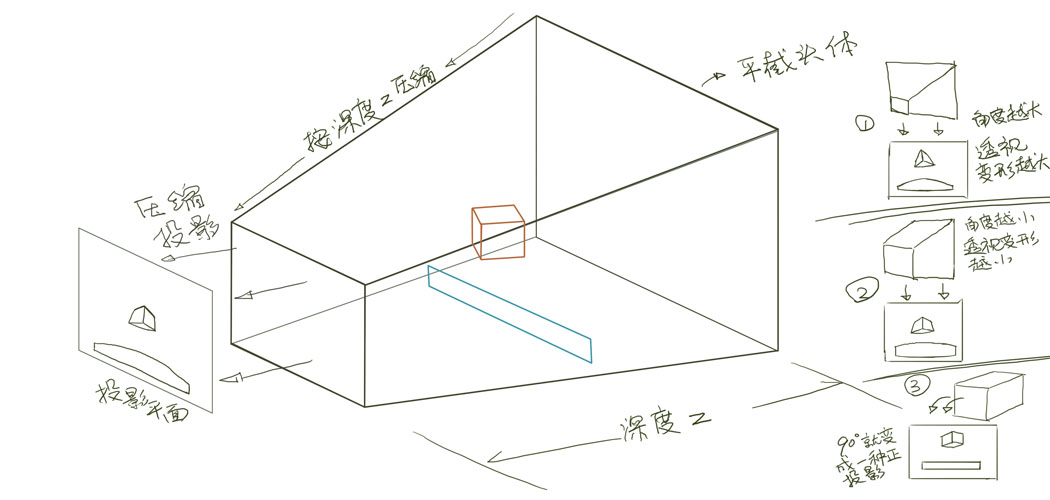 再回到楼主的理论···我说的验证是这个意思,下面这个一点透视图中两个小方块是画成2点透视还是3点透视? 图片如下: 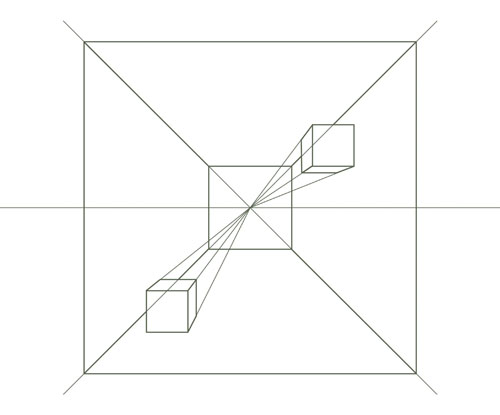
编辑历史:[此帖最近一次被 shadeIsland 编辑过(编辑时间:2008-12-1 12:55:33)]
|

飘然忽临
职务:普通成员
等级:1
金币:1.0
发贴:12
注册:2005/8/15 17:56:48
|
#282008/12/1 14:51:12
回复SII
真是苦口婆心啊,我都受益匪浅了。
楼主不会认真听你的意见的,一开始他就没想听你说,只想你听他说。他确实心态有问题,还没有达到成熟的阶段。遇到问题,一个成熟的人会不停的给自己找毛病,也就是能会反省。不成熟的人则不停的在别人身上找原因,还有一个就是他学识不够,很浮躁,没有耐心真正搞懂,在一知半解状况就开始自命不凡。估计在这发帖之前就得意一段时候了,大概总有一些初学者被他搅晕过。没想5d藏龙卧虎高手云集,几乎没人搅晕,还不时受到点戏谑。现在焦躁多于得意了。
跟他说这么多还不如让他好好去看看书,透视的书他是看不下去了,就看摄影的书,什么聚焦,焦距,长焦,广角的,去看医学的书,特别是眼睛构造的,去看物理的,了解光线,电磁波,引力,物理光学和几何光学,因为没有光线就没有形状和色彩。
想来他也没有耐心看懂这么多书,会说我也说远了。非常同意小葱的话:结婚吧,结婚就会清醒了。哈哈,经典!
|

~~e.灵~~
职务:普通成员
等级:3
金币:5.0
发贴:591
注册:2005/9/9 8:57:34
|
#292008/12/5 0:05:06
晕,很晕,相当晕。。。。
都是被楼主搞晕的。。。
你看,我晕的说胡话了吧:
照定理1所说:立方体---三面三透视
得出:立方体,三面三透视根本就不可能有平行边的存在
如楼主认为定理1正确的话。。。
那根本就没定理2什么事了。。。
因为所举例那两图照定理1来说是根本不存在的。。。
如楼主竖持认为定理2和定理1一样是正确的话...可能还要麻烦楼主再花点心思证明一下长方体和正方体不属于立方体。。。
我真的很晕了。。。所以呀我说的是对是错都别拍我了...
|

mark
职务:普通成员
等级:1
金币:0.0
发贴:237
注册:2008/5/19 7:34:56
|
#302008/12/5 10:51:47
楼主很搞笑哈。图8的中间截掉不就是图7嘛。 
|




